Limit of a function: Definition, Types, and Examples
Modern mathematics is built on the idea of the limit. The concept of limit is employed in all branches of calculus, such as integral and deferential, and has several real-world applications. Prior to developing limits, we must first determine the instantaneous rate of change, approximate calculation area, and volume.
Limits describe the behavior of a function at an approaching value of the function’s independent variables. In this article, we will look at the definition, types, and graphic representation of a function’s limit. We also go through the limits of the Univariate and Bivariate functions.
Limit of a function:
In mathematics, a Limit gives us a particular value of a function when we move closer to a particular value of a variable.
Let us have a function f(y) where y is approaching “a” then the function f(y) has a limit L.
Limy→a f(y) = L
- f(y) is a function with y as the independent variable.
- “a” is the approaching value.
- L is the limit of the function
Types of limits:
There are three types of limits regarding its approaching the path towards the limit.
- Right-Hand limit
- Left- Hand limit
- Two-sided limit
We will discuss the concept of these three types one by one.
1. Right–hand limit:
Let Limy→a+ denote the limit as y goes towards “a” for all values taking greater than a point “a”. Simply, we approach a from the right side, and then the limit is called the right-hand limit.
The Notation is:
Limy→a+ f(y) = L
The positive sign shows the direction means it’s Right-Hand side.
2. Left-hand limit
Let Limy→a– denote the limit as y goes towards “a” for all values taking less than a point c. simply, we approach c from the left side, and then the limit is called the left-hand limit.
The Notation is:
Limy→a– f(y) = L
The negative sign shows the direction which means it’s the Left-Hand side.
3. Two-sided limit
The limit that holds for both right-hand and left-hand limits. Its means that both limits are equal. It is denoted as
Limy→a f(y) = L
When does the limit exist?
The limit of a function is not necessary always exciting. If the limit excites then it must be satisfied a condition.
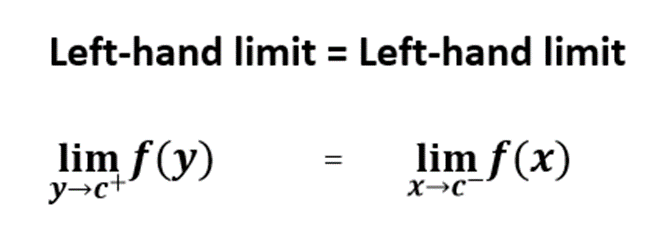
Examples of limit
We solve some examples to understand the limit problems.
Example 1:
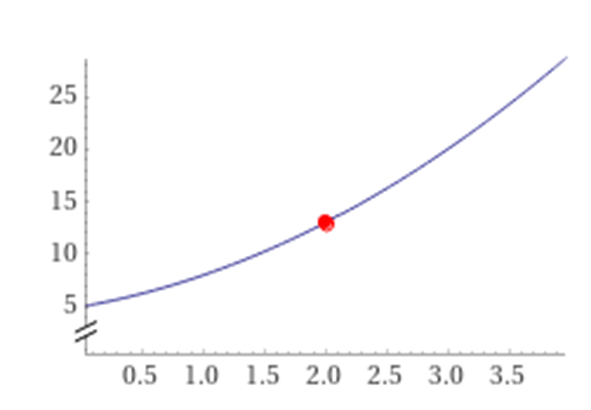
Find both the right-hand limit and left-hand limit of the function 2x + 5 + x^2 where the limiting value is x = 2
Solution:
Step 1: Write the function in the limit form.
Limx→2 [2x + 5 + x^2]
Step 2: For the Right-hand Limit We use the Plus sign on the limiting value
Limx→2+ [2x + 5 + x^2]
Step 3: Using the limit rule we apply the limit on every value
Limx→2+ [2x] + Limx→2+ [5] + Limx→2+ [x^2]
Step 4: Taking the coefficients outside the limit
2Limx→2+ [x] + Limx→2+ [5] + Limx→2+ [x^2]
Step 5: Now apply the limit
2(2) + 5(1) +2^2
4+5+4
13
Step 6: For the Left-hand Limit We use the minus sign on the limiting value
Limx→2– [2x + 5 + x^2]
Step 7: Using the limit rule we apply the limit on every value
Limx→2– [2x] + Limx→2– [5] + Limx→2– [x^2]
Step 8: Taking the coefficients outside the limit
2 Limx→2– [x] + Limx→2– [5] + Limx→2– [x^2]
Step 9: Now apply the limit
2(2) + 5(1) +2^2
4+5+4
13
Graph: From x= 0.004 to 4
Example 2:
Find the Limit of the function (x^2-4)/(x-2) at x = 2.
Solution
Step 1: Write the function in the form of limit
Limx→2 (x^2-4)/(x-2)
Step 2: We are not able to put the value of the limit because the 0/0 form occurs. We first solve algebraically expressions
Limx→2 (x+2) (x-2)/(x-2)
Step 3: After canceling the factor (x-2)
Limx→2 (x+2)
Step 4: Apply the limit now
= (2+2)
= 4
A limit calculator can also be used to evaluate the limit of a function.
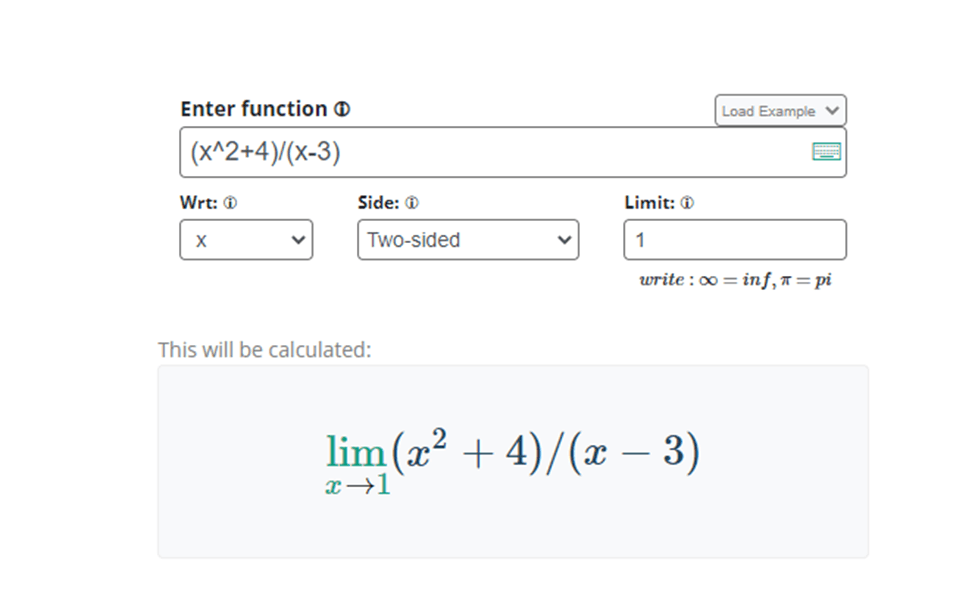
To calculate the limit, we have to follow some steps:
- Enter the function in give box.
- Select the name of the variable in the function or limiting variable.
- Select the type of limit you desire.
- Select the value of the limit.
The bottom box will show the right form of the input.
Example 3:
Find the limit of a function (5x+2x^2-3)/(x+3) at x approaches 2.
Solution
Step 1: Write the function in limit notation
Limx→-3 (5x+2x^2-3)/(x+3)
Step 2: We are not able to put the limit now. First, we use the algebraic method of simplifying the expression.
Factorization of 5x+2x^2-3 = (2x – 1) (x + 3)
Limx→-3 (2x – 1) (x + 3)/(x+3)
Step 3: After the simplification we have
Limx→-3 (2x – 1)
Step 4: Now put the limit in the function
= (2(-3) – 1)
= -6 – 1
= – 7
Example 4:
Find the limit of a function sin(7y)/y at y approaches 0.
Solution
Step 1: Write the function in limit notation
Limy→0 sin(7y)/y
Step 2: We are not able to put the limit now. First, we use the L’ Hospital rule method of simplifying the expression.
Limy→0 7*cos(7y)/1 taking the derivative of nominator and denominator.
Step 3: After the simplification we have
Limy→0 7*cos(7y)
Step 4: Now put the limit in the function
= 7 * cos (7*0)
= 7 *1
= 7
Applications of limit:
- Because limits are required to establish differential calculus, every application of differential equations implies the existence of the limits defining the terms in the equations.
- Limits are required in integral calculus since an integral is across a range of variables, which determine the integrations’ limits.
- The strength of electric, magnetic or gravitational fields.
- Object regions, forces, and eights
- Real-life limits are employed whenever there is a real-world application approach to a steady-state solution. As an example, a chemical reaction in a breaker might begin with two chemicals that combine to generate a new compound over time. As the time approaches infinity, the amount of the new compound is the limit of a function.
Similarly, if you put an ice cube in a glass of warm water and measure the temperature over time, the temperature will ultimately approach the ambient temperature where the glass is kept. As time passes, measuring the temperature becomes more difficult.
Summary:
In this article, we have learned about the limits, types of limits, examples, and applications in the different fields. Now you are familiar with how to solve different types of problems with limits.







